1. 激活函数
1. ReLU
线性整流函数(Linear rectification function), 又称修正线性单元, 是一种人工神经网络中常用的激活函数(activation function), 通常指代以斜坡函数及其变种为代表的非线性函数.
2. Sigmoid
-
缺点
sigmoid有一个梯度消失的问题, $|z|>4$(变量值很大或很小)的时候, 梯度就快消失了(趋近于0).
3. Tanh
$$ f(x)=\tanh (x)=\frac{\left(e^{x}-e^{-x}\right)}{\left(e^{x}+e^{-x}\right)} $$
4. Logistic Regression (LR 逻辑回归)
-
sigmoid函数
-
LR 模型是用线性回归模型的结果逼近真实标记 ($Y=1$ ) 的对数几率 (log odds,logit). 所谓的几率表示事件发生的概率 $P(Y=1|x)$ 与事件不发生的概率 $P(Y=0|x)$ 之比
$$ odds=\frac{P(Y=1|x)}{1-P(Y=1|x)} $$那么对数几率就是对几率取自然对数的结果
$$ \text { logit(odds) }=\ln \frac{P(Y=1 \mid x)}{1-P(Y=1 \mid x)}=w^{T} x + b $$ -
给定一组训练数据, 要求解上述的条件概率分布, 可以应用极大似然估计法 (Maximum Likelihood Estimation, MLE) 估计模型的参数. 极大似然估计, 即是对样本的似然函数 L 进行求参.
$$ L\left(x_{1}, x_{2}, \cdots, x_{n} ; \hat{\theta}\right)=\underset{\theta \in \Theta}{max}L\left(x_{1}, x_{2}, \cdots, x_{n} ; \theta\right) $$令 $P(Y=1 \mid x)=\pi(x), P(Y=0 \mid x)=1-\pi(x)$, 似然函数为:
$$ \prod_{i=1}^{n}\left[\pi\left(x_{i}\right)\right]^{y_{i}}\left[1-\pi\left(x_{i}\right)\right]^{1-y_{i}} $$对数似然函数(求最大化):
$$ L(w)=\sum_{i=1}^{n}\left[y_{i} \log \pi\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi\left(x_{i}\right)\right)\right] $$- $\pi(x)=\frac{e^{w^{T} x}}{1+e^{w^{T} x}}$
- $w=\left(w^{(1)}, w^{(2)}, \cdots, w^{(d)}, b\right)^{T} \in \mathbb{R}^{d+1}$
- $x=\left(x^{(1)}, x^{(2)}, \cdots, x^{(d)}, 1\right)^{T} \in \mathbb{R}^{d+1}$
最后的优化问题（转化为最小化）：
$$ \underset{w}{min}-\frac{1}{n} \sum_{i=1}^{n}\left[y_{i} \log \pi_{w}\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-\pi_{w}\left(x_{i}\right)\right)\right] $$针对上述最小化问题，采用 Newton method, quasi-Newton method (BFGS, L-BFGS), conjugate gradient 或者梯度下降法 (引入超参数 $\alpha$ ) , SGD 等等求都可以.
之后就是求解.
5. 多项逻辑回归模型(Multinomial Logistic Regression; softmax regression)
-
Softmax Regression 与 logistic regression 的联系
softmax逻辑回归就是多分类的逻辑回归
详细推导
2. 损失函数
- 损失函数的目的: 度量真实值和预测值之间的距离
2.1. 交叉熵(cross entropy)
2.1.1. cross entropy
-
公式推导过程
$$ \begin{aligned}\operatorname{argmax} \log \prod_{\mathrm{n}} \prod_{\mathrm{i}} \hat{Y}_{i}^{Y_{i}}&=\operatorname{argmax} \sum_{n} \sum_{i} Y_{i} \log \hat{Y}_{i}\\&=\operatorname{argmin}-\sum_{n} \sum_{i} Y_{i} \log \hat{Y}_{i}\end{aligned} $$
- $n$表示训练样本数; $i$表示分类数量. 因为只要找到最值就可以了, 所有这里是额外加一个$log$的. 利用$log$似然函数的特性, 把连乘提到$log$左边变成连加; 加上负号求最小值.
-
categorial_crossentropy函数和sparse_categorial_crossentropy函数:- 相同之处在于它们的 $y$ 都在 $(0,1)$ 之间
- 不同在于$Y_i$:
- 如果 $Y_i$ 的结果是one-hot encoded, 就是用
categorical_crossentropy. 例(三分类问题): $[1,0,0] , [0,1,0], [0,0,1]$. - 如果 $Y_i$ 的结果是整型, 使用
sparse_categorical_crossentropy. 例(三分类问题): $[1], [2], [3]$.
- 如果 $Y_i$ 的结果是one-hot encoded, 就是用
2.1.2. Binary cross entropy
-
二元交叉熵是二分类问题中常用的一个Loss损失函数, 是用来评判一个二分类模型预测结果的好坏程度. 公式如下:
$$ loss=-\frac{1}{N} \sum_{i=1}^{N} \left[y_{i} \cdot \log \left(p\left(y_{i}\right)\right)+\left(1-y_{i}\right) \cdot \log \left(1-p\left(y_{i}\right)\right)\right] $$- 其中, $y_i$ 是二元标签 0 或者 1, $p(y_i)$ 是模型的预测值为标签 $y_i$ 的概率
- 之所以加负号是因为概率在$(0,1)$, 取log之后是负的, 用负数表示信息不符合我们的认知逻辑，所以取负让结果为正.
- 就是说模型预测值越接近于gt值, loss越小; 越远离gt值, loss越大.
-
对于标签 $y$ 为 1 的情况, 如果预测值 $p(y)$ 趋近于 1, 那么损失函数的值应当趋近于 0. 反之, 如果此时预测值 $p(y)$ 趋近于 0, 那么损失函数的值为 $\infty$. 如下图所示.
-
对于标签 $y$ 为 0 的情况如下
-
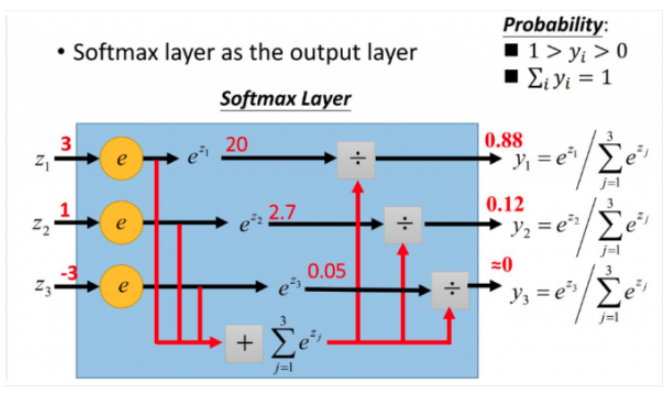
2.2. Softmax (归一化指数函数)
$f_{i}(\vec{x})=\frac{e^{x_{i}}}{\sum_{j=1}^{J} e^{x_{j}}} \quad \text { for } i=1, \ldots, J$
将原本的输出映射到区间$(0,1)$之间, 所有的值和为1
算是一种概率
好处:
-
求导方便
-
好结果和坏结果更显著
梯度下降时更新梯度, 由于网络末尾需要softmax函数计算结果$a$.
-
交叉熵函数的简单形式:
$\text { Loss }=-\sum_{i} y_{i} \ln a_{i}$
正向和反向求导时就很方便
-
-
损失函数推导过程
3. 过拟合问题
当讨论到模型的过拟合问题时, 不妨对算法的期望泛化误差进行讨论。我们已经知道: 泛化误差可 以分解为 bias, variance, noise 之和。
偏差 (bias) 衡量模型的期望预测与真实结果的偏离程度（模型的拟合能力）；方差 (variance) 衡量了同样大小的训练集的变动所导致的学习性能的变化, 即刻画了数据扰动 （数据变化对模型预测能力）所造成的影响（或者理解为在测试集上的表现）。噪声表达了在 当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度.
- 过拟合: low bias, high variance
- 欠拟合: high bias, low varience
3.1. 一般处理方法
- 减少特征的数量: 人工篮选特征、嵌入式选择
- 正则化：保持所有特征当时减小或者增大特征参数 $w^{(i)}$, 使得所有变量对最终的预测只贡献一 点比例
-
这里一般采用L1或L2正则化：(损失函数推导见拓展部分)
$$ \begin{gathered}\min _{w, c}\|w||_1 + C \sum_{i=1}^n \log \left(\exp \left(-y_i\left(x_i^T w+c\right)\right)+1\right) \\\min _{w, c} \frac{1}{2} w^T w + C \sum_{i=1}^n \log \left(\exp \left(-y_i\left(x_i^T w+c\right)\right)+1\right)\end{gathered} $$
4. Dropout
- 以一定的概率随机地“临时丢弃”一部分神经元节点.
- 优点, 解决过拟合的原因:
- 训练时:
- 减小网络的大小
- 减少神经元之间复杂的共适应关系(co-adaptations), 这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在某个特定特征下才有效果的情况.
- 人工神经网络的一个核心思想是分布式表征(Distributed Representation), 当我们表述一个概念的时候, 神经元和概念之间不是一对一对应映射(map)存储的，它们之间的关系是多对多。当一个节点发生故障的时候, 其他对应的节点能表达概念.
- 每次迭代所得到的不同结构的神经网络, 比只在单个健全网络上进行特征学习, 其泛化能力来得更加健壮.
- 测试时:
- 将参与学习的节点和那些被隐藏的节点以概率p加权求和，综合计算得到网络的输出。(算是一种集成学习(Ensemble Learning))
- 训练时:
- 训练阶段每个神经元以概率p被保留
- 测试阶段每个神经元都激活, 权重W要乘以p, 输出pW
- 因为输入将被dropout的神经元的值为$w$, 训练时dropout之后的期望是$E=pw+(1-p)*0$, 在预测阶段总是激活, 所以为了保持相同的输出期望, 所以$w \to pw$.
5. 目标函数, 代价函数, 损失函数
- 代价函数:
- 代价函数=损失函数, loss function越小, 标识模型对数据的拟合越好
- 目标函数:
- 在代价函数的最优化经验风险的基础上加入优化结构风险策略(eg: L2正则化)的函数表达式. 不加结构风险策略时, 目标函数就与代价函数一致了.
6. 损失函数的使用场景
7. k-fold交叉验证 Method of Stacking
- (左半边) 训练时每个model都用k-fold cross validation训练得到k个模型，测试时每个model的k个模型预测测试集得到的结果取平均
- (右半边) 训练时使用level2 model训练 验证集的合集和训练集，测试时使用level2 model来预测