type
status
date
slug
summary
tags
category
icon
password
1. 汉诺塔问题
- 问题: 将汉诺塔从A移动到C, 小圆盘必须在大圆盘上面.

- 分析:
可以将最底下的一块圆盘作为独立个体, 上面的所有圆盘作为另一个个体. 则整个汉诺塔的移动步骤如下.

算法实现:
2. 查找
2.1. 顺序查找
2.2. 二分查找
3. 排序算法

1.1. 简单
1.1.1. 冒泡排序
- 像气泡向上冒一样, 想象列表竖直.
- 第0轮: 从列表i=0位置开始. 如果最底部(i=0)的数字A比上一个数B大, 就互换位置. 再将A与上一个数C对比, 以此类推.
- 第1轮: 从列表i=1位置开始.
- 第len(list)-1轮: 从列表i=len(list)-1位置开始.
1.1.2. 选择排序
- 遍历找最小
1.1.3. 插入排序
- 从左边开始遍历, 像打牌时的理牌一样操作.
- 提取遍历到的数, 将比它大的数各右移一格, 这个数插入空档中.


1.2. 困难
1.2.1. 快速排序
缺点: 递归的层数是有限制的, windows下限制为998. 修改限制后能到达3929层左右. 无法处理更长的列表

时间复杂度推导
- 每一层的partition各自的时间复杂度是O(n), 如第2层每个partition的时间复杂度都是O(8).
- 一共有logn层
- 得出总共的时间复杂度为O(nlogn)

代码
1.2.2. 堆排序
树与二叉树
概念
- 根节点, 叶子节点
- 树的深度
- 树的度(同一深度最多的子节点个数)
- 孩子节点和父节点
- 子树
- 树是一种数据结构
- 树是由n个节点组成的集合
- if n=0, 这是一颗空树
- if n>0, 存在一个节点作为树的根节点, 其他节点可以分为m个集合, 每个集合本身又是一棵树
二叉树的顺序存储方式
- 二叉树的每层节点个数
- 父节点与左孩子节点的编号下标关系
- 父节点与右孩子节点的编号下标关系
- 从孩子节点推断父节点的编号下标
- 大根堆满足:
- 完全二叉树
- 任一节点都比其孩子节点大
- 小根堆满足:
- 完全二叉树
- 任一节点都比其孩子节点小
堆的向下取数
- 从父节点推算子节点
- 从最后一个非子节点开始(需要推断父节点位置)
堆排序
- 建立堆
从最后一个叶子节点开始向上调整
- 得到对顶元素, 为最大元素
- 去掉堆顶, 将堆最后一个元素放到堆顶, 此时可通过一次调整重新使堆有序(就是挨个出数)
- 不使用额外空间: 去掉顶部元素9的时候, 将9移动到3的位置, 将堆的结尾指针移动到4.


- 堆顶元素为第二大元素
- 重复步骤3, 直到堆变空
实现堆排序代码
使用python内置库, 进行堆排序
堆排序topK问题
- 原理:
- 在列表中取k个元素, 用这些元素建立一个小根堆(堆顶是堆里最小的).
- 遍历剩下的列表, 元素小于堆顶的忽略, 大于堆顶的放在堆顶, 对堆进行调整.
- 性能
- 时间复杂度: O(nlogk)
代码实现
1.2.3. 归并排序
- 原理
- 分解: 将列表不断一分为二, 直到只剩一个元素
- 合并: 将有序列表归并, 直到合成一个列表

代码
4. 栈
- 原理:
- 只能从一端进出
- 后进先出
- 操作:
- 进栈: push
- 出栈: pop
- 取栈顶: gettop
栈的实现
括号匹配问题

5. 队列
- 原理
- 从队尾(rear)进, 从队头(front)出
- 先进先出
环形队列


代码
双向队列
- 队首队尾两端都支持双向队列
6. 栈和队列的应用 - 迷宫问题

栈 深度优先算法(DFS)
- 使用回溯法
- 从一个节点开始, 任意找下一个能走的点, 当找不到能走的点时, 退回上一个点寻找是否有其他方向的点
- 使用栈存储当前路径
代码实现
队列 广度优先算法(BFS)
- 从一个节点开始, 寻找所有接下来能继续走的点, 继续不断寻找, 直到找到出口
- 使用队列存储当前正在考虑的节点
代码实现
7. 链表
链表是由一系列节点组成的元素集合
链表的优点
- 链表在插入删除操作上快
- 链表的内存可以灵活分配, 没有栈和队列的容量限制
- 链表这种链式存储的数据结构对树和图的结构有很大的启发性
7.1. 创建单链表
- 头插法 头部插入新节点
- 节点中, item保存元素, next保存下一个节点的内存地址
- 从1开始, head移动到下一个节点

- 尾插法 尾部插入新节点
- 节点中, item保存元素, next保存下一个节点的内存地址
- 从1开始, head不动, tail移动到下一个节点

代码
7.2. 单链表插入
链表节点的插入. 将节点p插入链表的当前节点的下一个位置

- 将节点p的next指向当前节点的next位置
- 将当前节点的next指向节点p
7.3. 单链表删除
删除链表中的节点p. 需要将该节点的前一个节点作为当前节点.

- 将节点4赋值为p
- 当前节点的next指向下下个节点
- 删除节点p (回收内存)
7.4. 创建双向链表
单链表只能从头向尾操作, 但是双链表可以做双向操作

7.5. 双向链表插入

7.6. 双向链表删除

8. 二叉树
8.1. 创建二叉树

代码
8.2. 二叉树的遍历
根和子节点的遍历顺序都是root → left →right

- 前序遍历: 根写在左边

- 中序遍历: 根写在中间

- 后序遍历: 根写在右边

- 层序遍历: 逐行扫描
- 算法实现需要使用队列, 先进先出.
- eg:
- E入队
- E出队AG入队
- A出队C入队, G出队F入队
- C出队BD入队, F出队
- BD出队
4种二叉树遍历代码
8.3. 二叉搜索树
二叉搜索树是一颗二叉树且满足性质:
- 设是二叉树的一个节点.
- 如果是左子树的一个节点, 那么
- 如果是右子树的一个节点, 那么
- 各节点数值都不相等.
插入操作
- 对比当前节点, 如果当前节点比插入数值小, 就对比当前节点的左孩子, 反之右孩子
- 如果没有孩子, 就插入
代码
查询操作
代码
删除操作
- 目标是叶子节点: 直接删除
- 目标只有一个孩子: 将此节点的父亲与孩子相连, 删除目标
- 目标有两个孩子: 将其右子树的最小节点n的值替换目标m的值,并删除n

二叉树 层序遍历
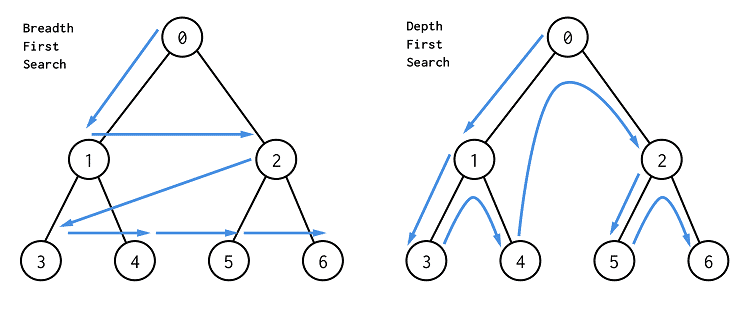
8.4. 深度优先搜索和广度优先搜索模板
BFS
- BFS使用队列,把每个还没有搜索到的点依次放入队列,然后再弹出队列的头部元素当做当前遍历点。
- 如果不需要确定当前遍历到了哪一层,BFS模板如下:
- 如果要确定当前遍历到了哪一层,BFS模板如下。
- level表示当前遍历到二叉树中的哪一层了,也可以理解为在一个图中,现在已经走了多少步了。
- size表示在当前遍历层有多少个元素,也就是队列中的元素数,我们把这些元素一次性遍历完,即把当前层的所有元素都向外走了一步。
DFS
- 递归
9. 动态规划
01背包问题
