Date
Aug 10, 2023
need_review
need_review
type
undo
undo
难度
困难
给你一个
n x n 整数矩阵 grid ,请你返回 非零偏移下降路径 数字和的最小值。非零偏移下降路径 定义为:从
grid 数组中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。示例 1:
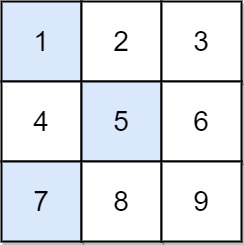
输入:grid = [[1,2,3],[4,5,6],[7,8,9]] 输出:13 解释: 所有非零偏移下降路径包括: [1,5,9], [1,5,7], [1,6,7], [1,6,8], [2,4,8], [2,4,9], [2,6,7], [2,6,8], [3,4,8], [3,4,9], [3,5,7], [3,5,9] 下降路径中数字和最小的是 [1,5,7] ,所以答案是 13 。
示例 2:
输入:grid = [[7]] 输出:7
提示:
n == grid.length == grid[i].length
1 <= n <= 200
99 <= grid[i][j] <= 99
解法1
递归 bfs 返回时找到最小的和
回溯的时候, 记得加上当前值, 时间复杂度为, 空间复杂度为
class Solution: def minFallingPathSum(self, grid: List[List[int]]) -> int: # 这个函数的input不可以做递归函数, 需要当前数的index def recur(grid, index): # 返回条件 if len(grid) == 0: return 0 # 递归 tmp_min = 200 # 矩阵中的值不会大于100, 两数相加不会大于200 for i in range(len(grid[0])): if i != index: # 递归矩阵从下一行开始 child_sum = recur(grid[1:], i) # 对比当前(最小数, 回溯值+当前值) tmp_min = min(tmp_min, child_sum + grid[0][i]) return tmp_min return recur(grid, -1)
超时
解法2
使用动态规划, 状态矩阵记录加法结果. 时间复杂度为, 空间复杂度为
class Solution: def minFallingPathSum(self, grid: List[List[int]]) -> int: length = len(grid) # 建立一个和grid相同大小的状态矩阵, 保存最小值 dp = [[0] * length for _ in range(length)] for i in range(length - 1, -1, -1): # 从最后一行开始倒序 for j in range(length): # 从左向右遍历 if i == length - 1: # 如果这是矩阵最后一行, 不需要操作(因为它下面是空的) dp[i][j] = grid[i][j] else: # 找到下一行中最小的非零偏移, 与当前值相加, 写入状态矩阵 tmp_min = min([dp[i+1][k] for k in range(length) if k != j]) dp[i][j] = grid[i][j] + tmp_min return min(dp[0])
